Chemical Kinetics
Upon completion of this exercise, you should be able to:
- Describe the rationale and techniques involved in accelerated stability testing. Explain how data at elevated temperatures is related to stability of the product at room temperature.
- Differentiate between zero, first, and second order reactions and reactions rates.
- Given drug degradation data for a compound, and the first order rate equation, construct an Arrhenius plot and determine:
- the activation energy for the degradation reaction.
- the first order rate constant for the degradation reaction at 25°C.
- an appropriate shelf-life for the product (usually T90 at 25°C).
The chemical stability of a drug in the desired dosage form is of great importance since therapeutic problems may result from poor drug stability. The net result of drug instability is that the patient does not receive the proper dose of the active drug entity, and therefore, the full therapeutic effect of the drug is not realized. Additionally, drug decomposition may yield toxic by-products which endanger the patient.
The industrial pharmacist must choose dosage form excipients and storage conditions that result in an acceptable fraction (generally 90-95% or greater) of the drug being present for an acceptable length of time. The hospital or retail pharmacist must observe the manufacturers’ storage recommendations. He/she must also be aware of the types of degradation that a particular drug is subject to since drug products are frequently repackaged at the time of dispensing.
When a new drug product is being formulated, it is desirable to determine the stability of the drug entity in the drug product so that a shelf life or expiration date may be assigned to the product. The shelf-life is the length of time required for the product potency to be reduced to some percentage of its original value. For most products, this is the T90 or time at which the product retains 90% of its original potency. Although the drug’s stability at room temperature is of primary interest, a stability study at room temperature would take too long to be useful as a screening procedure for new formulations. Therefore, such screening studies are conducted at elevated temperatures in accordance with the Arrhenius equation:
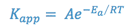
where,

The Arrhenius equation can be rewritten as:
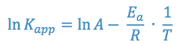
Again, an equation of the form y = mx + b is generated, indicating that a semi-log plot of Kapp vs. the reciprocal of the absolute temperature (1/T) should yield a straight line with a negative slope equal to -Ea/R. This line can be extrapolated to the value of 1/T that corresponds to room temperature and the predicted rate constant for the reaction at room temperature can be taken from the y- axis.
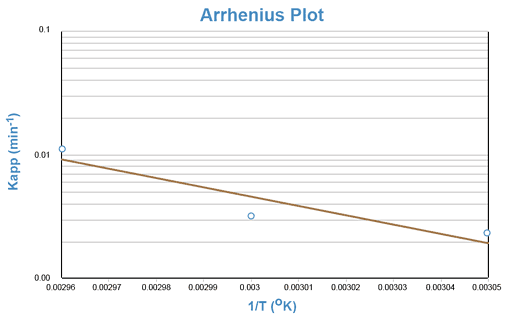
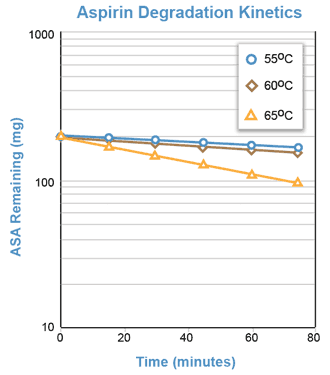
Although the degradation of aspirin in a solution buffered at pH = 7.5 occurs too slowly at room temperature to be adequately studied during one laboratory period, the reaction proceeds rapidly at temperatures of 50°C and above. The reaction will be conducted at approximately 55°, 60°, and 65°C.
Hydrolysis of the drug entity can be a major factor in the instability of solutions. Aspirin, for example, undergoes hydrolysis with the resultant degradation products being salicylic acid and acetic acid. The rate of this reaction is said to be second order, since it is dependent not only upon the aspirin concentration, but upon solution pH (i.e. the hydronium ion concentration at solution pH values less than approximately 2.5 or the concentration of hydroxyl ion at solution pH values greater than approximately 7.0). At pH = 7.5, the rate expression for the hydrolysis of aspirin may be written:
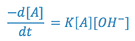
where,

If the solution is buffered so that the hydroxyl ion concentration remains essentially constant, the rate expression may be rewritten as:
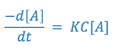
where,

Since two constants can always be combined into one constant, the above expression is equal to:
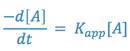
where,

From the above equation, it can be seen that the degradation of aspirin in a solution buffered at pH = 7.5 will follow first order kinetics; that is, the reaction will appear to be a first order reaction, dependent only on the concentration of one reactant; i.e., aspirin.
The integrated form of a first order rate expression is:
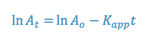
where,

This equation is of the form:

where,

For the hydrolysis of aspirin in buffered solution (pH = 7.5), a semi-log plot of the aspirin concentration remaining versus time should yield a straight line with a negative slope equal to -Kapp.
The experimentally determined first order rate constant (![]() ) can be related to the true second order rate constant by the expression:
) can be related to the true second order rate constant by the expression:
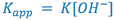
The pseudo first order degradation of aspirin in a solution buffered at pH = 7.5 can be followed by measuring the increasing concentration of salicylic acid spectrophotometrically.
One mole of salicylic acid is produced when one mole of aspirin degrades; so, using the ratio of the molecular weights of aspirin to salicylic acid, we can determine the weight of aspirin degraded for each mg of salicylic acid produced.
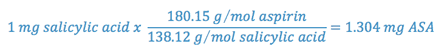
Thus, each milligram of salicylic acid present represents the degradation of 1.304 milligrams of aspirin. Since the amount of aspirin initially present is known and since the amount of aspirin which has degraded can be determined, the amount of aspirin remaining can be calculated.